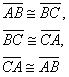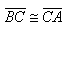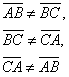CALCULANDO AREA Y PERIMETROS EN TRIANGULOS MEDIANTE GEOGEBRA

TRIÁNGULOS

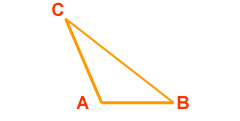
Triángulo es la figura plana formada por una poligonal cerrada de tres lados, o bien, la figura formada por tres rectas que se cortan, a los puntos de corte se les llama vértices.

Los ángulos del triángulo se designan con letras mayúsculas A,B, y C y los lados opuestos con a, b y c. La suma de los lados es el perímetro y notaremos por p el semiperímetro.

CLASIFICACIÓN DE TRIÁNGULOS SEGÚN LA MEDIDA DE SUS LADOS Y ÁNGULOS

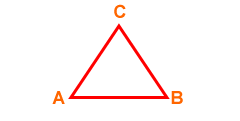
TRIÁNGULO EQUILÁTERO

El triángulo equilátero es aquel que tiene todos sus lados de la misma medida, en donde:

TRIÁNGULO ISÓSCELES

El triángulo isósceles es aquel que tiene sólo dos lados de igual medida.

TRIÁNGULO ESCALENO

El triángulo escaleno es aquel que tiene todos sus lados de distinta medida.

TRIÁNGULO ACUTÁNGULO

El triángulo acutángulo es aquel que tiene todos sus ángulos agudos.

TRIÁNGULO RECTÁNGULO

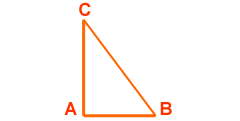
El triángulo rectángulo es aquel que tiene un ángulo recto (< CAB).

TRIÁNGULO OBTUSÁNGULO

El triángulo obtusángulo es aquel que tiene un ángulo obtuso, tal como se muestra a continuación:

ÁREA Y PERÍMETRO

Comenzaremos por el concepto más sencillo, vale decir por aprender qué es y cómo se halla el Perímetro de un triángulo

El perímetro de un triángulo es igual a la suma de la longitud de sus lados. Calcularlo, entonces, es así de sencillo: debes conocer o medir el valor de cada lado y simpleme

nte los sumas.

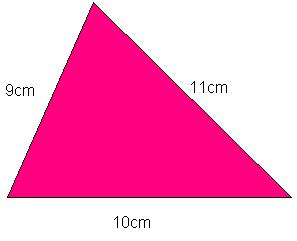Ejemplo: si se nos pidiera calcular el perímetro del triángulo de la figura, simplemente habríamos de sumar el valor de sus lados. Así las cosas sería 11cm + 10cm + 9cm = 29 cm. El perímetro del triángulo de la figura es de 29 cm.

Algunos casos especiales son, por ejemplo, el triángulo equilátero, en el cual para hallar el perímetro simplemente multiplicas l * 3, es decir lado * 3, porque como sabemos, en este caso sus tres lados son iguales. Si hablamos de un triángulo isósceles, una fórmula posible sería lado *2 + base, pero sin ninguna duda, lo más sencillo y seguro es considerar a todos los triángulos como si fueran escalenos y simplemente sumar los tres lados.

Área de un triángulo

El área de un triángulo se calcula multiplicando base por altura dividido por 2. A veces cuesta determinar cuál es la altura y para que sea sencillo para ti encontrarla, te recomiendo trazarla como una línea auxiliar, considerando que se trata de la recta perpendicular trazada desde cualquier vértice a su lado opuesto (o su prolongación).

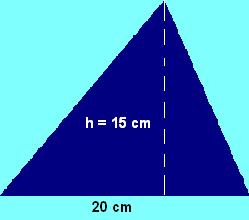
Ejemplo: si se trata de calcular el área del triángulo de la figura, debes multiplicar base por altura (que se simboliza por “h” de high en inglés) y dividir entre dos. Sería 20 * 15 /2, de modo que el resultado final, vale decir el área del triángulo en cuestión, es igual a 150 cm2.

Ahora bien, existen casos de otros triángulos donde trazar la altura no es tan sencillo o mejor dicho tan claro. Veamos otro caso donde es necesario trazar la altura hacia la prolongación de uno de los lados.

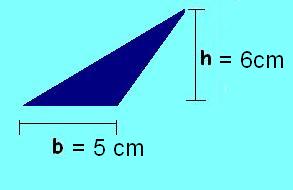Ejemplo: si te enfrentas al reto de calcular el área de un triángulo como el de la figura, en estos casos es necesario trazar la altura tal como muestra la imagen, es decir, desde el vértice superior hasta la prolongación de lo que visualmente es la base del triángulo. En este caso multiplicarías 6 cm * 5 cm /2 = 30 cm2.

Un ángulo y un lado son adyacentes cuando el vértice del ángulo está sobre el lado, y un lado y un ángulo son opuestos cuando el ángulo no tiene vértice en ese lado.

Área y perímetro de un triángulo.

UTILIZANDO GEOGEBRA PARA CALCULAR

ÁREA Y PERÍMETRO EN TRIÁNGULOS

Área[ <Vértice Inicial (punto)>, <Segundo Vértice (punto)> ..., <Vértice Final (punto)> ]: Calcula el área del polígono definido por los sucesivos puntos vértices.
Así área[ A, B, C ] calcula el área del triángulo definido por los vértices A, B y C.
Área[ <Polígono> ]: Establece el área del polígono indicado.

Nota:
De hecho, cuando se crea un polígono, se cuenta con el dato del valor correspondiente a su área.
Área[ <Cónica> ]: Calcula el área de la sección cónica dada (circunferencia o elipse).

Atención:
El resultado se registra para circunferencias o a elipses y queda indefinido para otras cónicas.

Área[ <Arco_{de circunferencia} o Sector_circular> ]: Calcula el área del sector circular dado o la del delimitado por el arco de circunferencia indicado.

Nota:
De hecho, cuando se crea un sector, se cuenta con el dato del valor correspondiente a su área.

Ejemplo:
Área[Sector[Circunferencia[D, E, F], J, G]] da un resultado acorde a la posición relativa de los puntos indicados.; Nota:
Para calcular el área entre dos funciones gráficas, se precisa el comando IntegralEntre.